In 2005, we published an article on the 'Crisis in Cosmology' by Harry Nielsen, which provoked some comment from readers. In addition to the original article, we publish as appendixes a letter that defends the main theories dominant in contemporary physics. This is followed by a reply that points out that the latest observations should at least lead scientists to question the validity of the Big Bang theory, a theory that dominates the thinking of mainstream physicists in spite of the all evidence. We also publish a second letter, supportive of Nielsen, commenting on the Olbers' paradox (explained in another appendix), which states that if galaxies and stars had existed for an infinite amount of time then the whole sky would look bright. This is also followed a reply from Nielsen.
An uncomfortable parallel can be drawn between the Big Bang story and the Christian myth of creation. At the root of the whole theory is faith, faith in things which cannot be seen or detected physically, such as an invisible form of matter and energy that is supposed to pervade the universe, or on a definite moment in time in which all matter as we know it came into being. The emphasis in theoretical physics and in mainstream cosmology is on pure thought and logic. Plasma cosmology on the other hand makes no assumption about the age of the universe; it places no limitations on the time available for large scale structures to form. The explanation for things that have occurred in the past lies in the processes that we see now, which in many cases we can explore in laboratory experiments. There is no effect without cause ‑ an infinite chain of cause and effect leads from now to the past.
For both the layman and the scientist the images produced by modern astronomical devices are a reminder of how astonishingly beautiful nature can be. What is immediately striking about them are the patterns of motion, patterns that are surprisingly similar to those that we see on earth, but on a cosmic scale. Huge swirling clouds of gas and dust roll through the space between the stars and the galaxies. Coils of hot gas explode from the remnants of a star. In every part of the universe, from our own Solar System to the most distant galaxies, we see evidence of change and motion. What is happening here? What is causing this?

The standard answer given by modern cosmologists is that what we see now in the movement of the stars and galaxies is the aftermath of a gigantic explosion which took place over 14 billion years ago. This is the Big Bang theory of the origin of the universe. But a flood of recent information from new terrestrial and space-borne telescopes has led many scientists to question this, the “standard model” of cosmology. A whole range of recent observations, of galactic structures, stellar and galactic ages, background radiation, the proportions of different elements in the universe, appear to contradict the predictions of the Big Bang theory. An increasing number of scientists believe that there are serious problems in this theory and there is a growing feeling that this part of science is in crisis.
In the summer, in Monção Portugal, a group of astronomers and physicists met to discuss the situation and to look at the alternatives. The meeting took place under the title “Crisis in Cosmology” and was the initiative of the “alternative cosmology group”. This is a group of scientists that includes the plasma physicist Eric Lerner, author of the book The Big Bang Never Happened .[1] Last year, this group published an open letter in New Scientist magazine that questioned the fundamental ideas of the Big Bang, and also pointed to the restrictions that funding bodies are placing on research into alternatives[2] The conference in Portugal was the practical outcome of the discussion in scientific circles that took place after the publication of the letter.
In Reason in Revolt,[3] Alan Woods and Ted Grant also pointed to the scientific and philosophical inconsistencies that exist in Big Bang theory. All the evidence that has emerged since then, and in particular the most recent observations, confirm their analysis – that the idea of the Big Bang is flawed, is inconsistent with a materialist and a dialectical view of the universe, and that ultimately its supporters will be forced to accept that it has failed to explain the known facts.
Microwave background radiation and inflation
One of the supposed successes of Big Bang theory is its explanation of the “cosmic microwave background radiation”, which was first observed in 1964. This is a low amplitude radio signal at frequencies similar to those used in a microwave oven, which is seen in all directions in space. Big Bang supporters say that this is the left over energy from the Big Bang explosion.
In fact when the background radiation was first discovered it was inconsistent with the version of the Big Bang theory that existed at that time. The theory could not explain why the radiation was so uniform across the sky, compared to the lumpiness of matter in the universe, clustered into clouds of dust and gas, galaxies and stars. But Big Bang theorists have at several times in the history of the theory been forced to adjust their ideas when they have conflicted with new evidence. In this case, in order to explain the smoothness of the background radiation, it was necessary to invent the idea of cosmic inflation. This is described in the following extract from the Wikipedia entry on the topic:
“Cosmic inflation is the idea, first proposed by Alan Guth in 1981, that the nascent universe passed through a phase of exponential expansion (the inflationary epoch) that was driven by a negative pressure vacuum energy density… As a direct consequence of this expansion, all of the observable universe originated in a small causally-connected region. Quantum fluctuations in this microscopic region, magnified to cosmic size, then became the seeds for the growth of the structure of the universe. The particle responsible for inflation is generally called the inflaton.”
This is meant to be a serious attempt to explain fundamental questions about the origin of the universe, but it is impossible to take passages like this seriously. The background radiation is smooth, so first the universe must expand very quickly and smoothly, driven by a “negative pressure vacuum energy density”, but the galaxies are lumpy, so everything then slowed down to give matter time to clump together – but randomly, as the result of “quantum fluctuations” which somehow become magnified into the universe we know. All of this is mediated by the “inflaton” – a particle that has never been observed (but presumably we are too late and have missed it). A science fiction writer could not do much better.[4]
Nonetheless, cosmic inflation became an accepted part of Big Bang theory. It preserved the theory by allowing its prediction of the cosmic radiation to be smoothed to match the observations. Much of what has been developed in the theory since then has been based on the “inflationary model”, and the current version of the Big Bang depends critically on this idea.
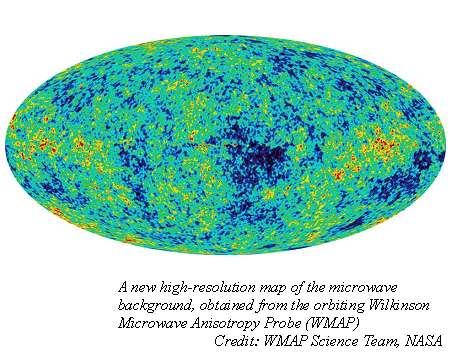
In 2003 results became available from a new satellite, the Wilkinson Microwave Anisotropy Probe (WMAP) which showed the cosmic radiation in more detail than previously. Initially, and again in the spirit of modern cosmology, the new results were described as a success for Big Bang theory and “a complete confirmation of the inflationary theory”. However subsequent analysis has shown the opposite.
One of the predictions from the inflationary theory is that the background radiation should be smooth apart from small random fluctuations. This prediction has been written into the textbooks, and has support from all the major proponents of the theory. Careful analysis of the WMAP results shows, however, that the radiation is not smooth. Glen Starkman presented results to the Portugal conference showing that not only are the fluctuations different from that predicted by Big Bang theory but they are aligned with the geometry of the solar system. Rather than being “cosmic” in origin – i.e. the left over energy from the Big Bang – it seems more likely that the radiation is light and radio waves from stars that has been scattered by dust and clouds in space, causing some of the radiation to line up with the local structure of our solar system and galaxy.
But the tendency to look for explanations in obscure theory is ingrained in modern cosmology. An astrophysics weblog discussing the WMAP results contained these recent entries:
“I have proposed an explanation in terms of many-sheeted space-time… See my article “Fluctuations of the microwave background as a support for the notion of many-sheeted space-time”. [Matti Pitkanen]
“Could this be explained by non-uniform distribution of mass in the universe? i.e. what if all the supposed dark matter is inside some giant black hole lurking somewhere, could that black hole affect cosmic microwave background photons in a way to produce such anomalies?” [Artem Khodush]
The discussion closed with the following:
“This is the problem with teaching and endorsing fantasies. Students start to think of fantastic (that is, absurdly unreal) scenarios instead of sticking to sane physics. The issue is that the data indicate an unexplained local contribution to the microwave background, after which the C in CMB [cosmic microwave background] is practically irrelevant, the Big Bang plain wrong, and inflation an opium smoker’s pipe dream.” [D R Lunsford]
Expansion and the red-shift
Further problems have emerged for Big Bang theory in its assumption that the universe is expanding as a result of the explosion at the beginning of time.
Edward Hubble, in 1929, was the first to notice a strange and unexpected behaviour in the light from distant objects which he interpreted as evidence of the expansion of the universe. Hubble saw certain sets of colours in the light that he could identify as belonging to specific elements. (Heated sodium gas, for example, always produces yellow light, as in street lamps, and other substances always generate or absorb colours that are characteristic of that substance.) But Hubble also noticed that the colours were shifted away from their normal position, towards the longer wavelengths at the red end of the light spectrum. Even more puzzling, the amount by which they were shifted was greater for galaxies that, judging by their brightness, were further away.
Hubble surmised that the red-shift of the colours was due to the light waves from the galaxies being stretched by movement away from the earth. A similar effect – the Doppler effect - occurs on earth when a source of light or sound moves; a moving train produces a high pitched sound when it approaches and a lower pitched sound as it moves away and stretches out the sound waves. But this interpretation of the red-shifts meant not only that the galaxies were moving away, but that the more distant galaxies were moving at the greatest speed. The galaxies were like dots on the surface of an inflating balloon - the universe was expanding.
This was the central observation that led to the idea of the Big Bang. In the motion of the galaxies, say the Big Bang supporters, we see the aftermath of a great explosion. Matter was at one time concentrated at one point, and is now rushing away from where the explosion occurred. This interpretation of the Hubble red-shift in terms of the expansion of the universe has become one of the cornerstones of Big Bang theory.
Eric Lerner presented a paper at the Portugal conference which seriously challenges this point of view. He has used images, aptly enough from the Hubble space telescope, to examine the surface brightness of the most distant known galaxies. The Big Bang theory makes predictions about how the surface brightness of objects should vary with distance which are different from the behaviour that would be expected in a non-expanding universe. His results show that the Big Bang predictions are dramatically wrong – distant galaxies are as much as several hundred times brighter than the Big Bang suggests:
“The data clearly show that the universe is not expanding, and that the redshift of light must be due to some other cause, perhaps in the properties of light itself. This also means that the universe that we can see is not limited in space or time—the most distant galaxies we see right now are 70 billion years old, much older than the supposed age of the Big Bang, and we will be able to see older and more distant ones with future telescopes.”
Further support for this point of view was presented in a paper by Thomas Andrews. He looked at distance estimates derived from the relative brightness of two different classes of objects: supernovae and the brightest galaxies in clusters of galaxies. He showed that the estimates from the supernovae contradicted those from the galaxies if the universe was assumed to be expanding. But when distances were computed assuming that the universe is not expanding the discrepancy between the two sets of distance estimates disappeared.
Age of the universe
Big Bang theory encounters some of its greatest difficulties due to its assumption of a “beginning of time”, a time when matter and motion emerged into the universe. Several studies have shown, however, that there is simply not enough time since the Big Bang for the formation of the large-scale structures that have been observed in clusters of distant galaxies. Francesco Sylosis-Labini presented results from a recent study that found structures in clusters of galaxies as large as 210 million light years in size; since the galaxy velocities are only 1/1500 of the speed of light it is impossible for structures of this sort to have formed in the time since the Big Bang. Other research using computer modelling has shown that even with the most favourable assumptions the large-scale structures that have been observed would require three to six times longer to form than the time that is supposed to have elapsed since the Big Bang.
Similarly, individual galaxies have been observed that are older than the Big Bang. The age of a galaxy can be estimated from the colour of the light generated by its stars; older and cooler stars produce more red light than young stars. Distant galaxies have been seen that, according to the colour of the light emitted by their stars, predate the Big Bang by as much as one billion years.
Big Bang theory has always had difficulties of this sort in reconciling observations of the universe with its prediction about the age of the universe. “Dark matter” – never observed, despite 20 years of expensive particle physics research ‑ was invented to explain how galaxies could be formed by gravitational collapse, given that there appears to be only 5% or so of the required density of matter in the universe to allow this to happen in the time since the Big Bang. But when it was discovered that the universe is apparently expanding at an accelerating rate it was necessary to quickly invent “dark energy”, to be turned on to accelerate the galaxies apart after the dark matter has finished its job of forming them. Now it has been suggested that large scale galactic structures could form if dark energy and dark matter are assumed to balance each other (although this would also make the universe 32 billion rather 14 billion years old – a small detail.) Eric Lerner reports, however, that the researchers responsible for this result “agree that this model is not at all realistic”.
Plasma cosmology
Astronomers and cosmologists are becoming increasingly aware of the role that plasmas and electromagnetism can play in a range of different phenomena in the universe. One of Eric Lerner’s presentations at the Portugal conference was an overview of plasma cosmology, the ideas developed initially by the plasma physicist Hannes Alfven.
Plasma is hot gas that has become “ionised” – negatively charged electrons have become separated from atoms leaving positively charged ions. An example of a plasma is the arc of a welding torch – free electrons and ions in the hot gas between the electrodes allow electric current to flow, producing heat, light and also radio waves which can interfere with nearby radio receivers. Perhaps as much as 99% of the matter in the universe is believed to exist in the form of plasma, either in the stars or in vast clouds of gas between the stars and the galaxies.

Plasma cosmologists believe that electromagnetic effects from plasma, which are ignored in conventional cosmology, can explain the effects for which Big Bang theorists are forced to invent never-observed entities such as dark matter and dark energy. Electrical currents in interstellar and intergalactic plasmas can generate magnetic forces that are as strong as gravitational forces, and it is these that can explain galaxy formation and structure without the need for dark matter or other absurdities. But conventional cosmology rarely considers anything other than gravitational effects.
Several participants at the conference referred to plasma-related effects in their presentations and in the general discussion. Donald Scott[5] pointed out in his paper, however, that main-stream astrophysicists often seem to be unaware of the basics of electromagnetic theory and that in this area too care is needed to avoid the tendency to invent false physics to fit theories: “Recently astrophysicists have been discovering (inventing) hypothetical entities and forces at an increasing rate. They have done so with impunity because these entities are not falsifiable – no in situ experiments are possible in remote space. But when experimentally verified laws of electrical science are disregarded or misinterpreted it is time to present a challenge – to initiate a dialog between the two camps that will resolve this contradiction.”
One of the unusual aspects of plasma cosmology is that it predicts a fractal distribution of matter throughout the universe. Fractals are objects that have repeating patterns at different scales from small to large; several papers at the conference discussed possible consequences of this behaviour. A fractal distribution implies areas empty of matter, voids between galaxies and clusters, will appear and reappear at ever larger scales. Since plasma cosmology makes no assumption about the age of the universe it places no limitations on the time available for such large scale structures to form.

Dark Matter
“Much of the mass of the universe is believed to exist in the dark sector. Determining the nature of this missing mass is one of the most important problems in modern cosmology. About 23% of the universe is thought to be composed of dark matter, and 73% is thought to consist of dark energy, an even stranger component distributed diffusely in space that likely cannot be thought of as ordinary particles.” [Wikipedia]
Most people when they paint themselves into a corner will admit their mistake and splash their way out. Mainstream cosmologists turn round and dismantle the corner brick by brick until the building comes down on top of them.
Faced with observations of the motion of galaxies that can’t be explained by gravity alone, it would seem reasonable to consider the possibility that electromagneticism might be responsible. After all, since science began physicists have been able to find only four different types of force: gravity, electromagnetism, and the strong and weak nuclear forces, the last two of which act only at very small sub-atomic distances. Unfortunately however, there is less kudos in working with the classical physics of electromagnetism than in an exposition of some unexpected consequence of general relativity, and general relativity only deals with gravity.
Dark matter was invented to produce the additional gravity for galaxies to form, and also to prevent existing galaxies from falling apart. The rotational speeds of many galaxies are too large for the gravity produced by the visible matter to hold them together. Rather than looking for an explanation for this in known physics, as the plasma cosmologists have done, Big Bang theorists instead have invented an invisible form of matter and energy that is supposed to pervade the universe, accounting for as much as 95% of the total. Unfortunately, despite its enormous contribution to gravity, dark matter in other respects “weakly interacts” with normal matter, weakly excusing its lack of appearance to date in any experimental tests. This has not prevented the science funding bodies from planning to spend yet more money in an elusive search for this invisible substance which supports so many scientific careers.
Dark matter is not so much dark as missing. Recent studies of the infra-red radiation from galaxies have made it possible to estimate the mass of the stars in those galaxies. The gravitational effects in these galaxies and in clusters of galaxies leave little room for the dark matter. For galaxies the visible matter can account for 2/3 of the observed gravitational effects, although for clusters of galaxies less of the required matter is visible, possibly because it is obscured by the large amount of dust and gas in those objects.
The scientific method
 There was a full conference session dealing with the question of how cosmologists and scientists in general should work in subjects such as cosmology where they are trying to understand very distant and inaccessible objects. Timothy Eastman pointed to the dangers that are inherent in the deductive approach that is common in cosmology and other parts of science, where explanations are derived from “laws of the universe” which are assumed to need no proof (and which can therefore be made up to fit the facts). One of the alternatives he suggested was computer-based “data-mining”, where computers are used to look for patterns in data without resorting to theory.
There was a full conference session dealing with the question of how cosmologists and scientists in general should work in subjects such as cosmology where they are trying to understand very distant and inaccessible objects. Timothy Eastman pointed to the dangers that are inherent in the deductive approach that is common in cosmology and other parts of science, where explanations are derived from “laws of the universe” which are assumed to need no proof (and which can therefore be made up to fit the facts). One of the alternatives he suggested was computer-based “data-mining”, where computers are used to look for patterns in data without resorting to theory.
The popularity of the deductive approach rests on the fact that in a few well understood areas of science it has been possible to summarise years of scientific work in an abstract and highly compressed form, using a small number of mathematical statements. An example is Maxwell’s laws of electromagnetism:


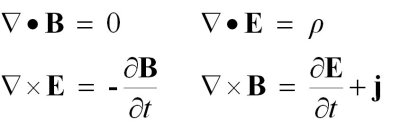
These symbols express the connection between an electric field E, magnetic field B, the electric charge density r and the electric current density j, together with their changes in space and time, which are represented by the operators ∇•, ∇ x ∂/∂t. From these equations, so the story goes, it is possible to use the rules associated with these mathematical symbols to derive all the known electromagnetic phenomena. For a mathematician or physicist this is a very attractive, almost seductive, proposition, where everything appears complete and consistent and everything can be understood, at least by the initiated, through application of the laws of logic and their expression in mathematics.
Unfortunately modern scientists have a tendency to forget that it has taken many years of practical work by many people to reach this point in our understanding of electromagnetics, and likewise in the relatively few other areas of science where similar generalisations have been possible. Maxwell’s equations are described as axioms – statements for which no proof or demonstration is required. But this is a very one-sided view, which starts with the end result of perhaps thousands of years of human and scientific development and ignores what has gone before as if it was irrelevant. To reach the point where even the idea of an electric field, or the mathematical representation of change with respect to time or space, has been established, explored, developed, applied, tested and shown to be useful has required contributions from countless numbers of scientists over a long period of time. The four equations that make up Maxwell’s equations decompose into many more physical and mathematical concepts, linked to and supported by the results from a whole range of scientific activity. If they are axiomatic, if they are the point of departure, why does it take perhaps 15 years or more of education, including several years of specialisation in mathematics and physics, before they can be used and understood?
The emphasis in theoretical physics and in mainstream cosmology is on deduction from axioms, on pure thought and logic. The Big Bang theory, with its lack of support in observation, shows the danger inherent in this approach. Yet it is the prevailing method in cosmology, taught and encouraged in the universities because it gives very clever people an opportunity to demonstrate their brilliance through asserting the absurd. First a sweeping generalisation, an axiom from which all else will be deduced. Then the brilliant exposition, the startling conclusions, the sweep of the hand, the modest bow of the head, the ripple of applause.
Then the problems, the fix-ups, the silencing of the opposition.
There is a further difficulty. “From these laws all known phenomena will be deduced.” Well, not quite. Only in the simplest cases, for the simplest geometry and for a small number of features/particles/components/actions (preferably no more than two). The skill of the practising physicist lies in finding the approximation that is good enough, twisting and turning the ideas and the mathematics to try to make it fit the complexity. The reality of most physical phenomena is that there are many interlinked features, all of which interact. And increasingly physicists are beginning to find that it is the interaction that is more important than the details of the physical laws. Transitions occur that are determined by the complexity itself regardless of the details of the physics; this is why a fractal model can work over many scales and different physical mechanisms. The physical axioms and their deductions not only become inadequate, they become irrelevant. More general laws emerge – the dialectical laws of quantity and quality, of the union of opposites and the negation of the negation.
A purely empirical approach, where the need for theory is denied, is equally one-sided. Learning from experiment, generalising the experience, and then putting that to test in new experiments is as fundamental to the development of scientific ideas as it is to the development of an individual. Practicing scientists, particularly in observational sciences such as cosmology or geophysics, are continually drawing ideas from their data, testing these ideas by applying them back to the data, and refining or changing their ideas. This is induction and deduction, simultaneously, not one or the other but both together.
For Eric Lerner the question of methodology in the development of scientific theories is as important as the details of the physics. In a recent interview[6]<!--[endif]--> he commented that: “The big break through of the scientific revolution of Galileo and Kepler is the notion that the laws of the cosmos, the physics and science of the cosmos, is the same as the science we observe here on earth”.
Big Bang theorists assert, for example, that “in the beginning” (and it is impossible to avoid biblical expressions of this sort) all matter in the universe was concentrated into one single point of infinite density. True, we cannot say this is impossible. But any similar phenomena have never been seen, in any experiment or observation, and there are other possibilities that can explain the movement of the galaxies, the background cosmic radiation, the proportion of light and heavy elements in the universe, and the other observations which the Big Bang theorists claim, incorrectly, to explain. Rather than asserting, with no evidence and in complete contradiction to what has been observed to date, that matter was compressed to a point, it would be better to say “if we take the situation to the limit of massive gravity we don’t know what happens, but it is unlikely that matter appears or disappears because we have never seen that”.
Knowledge can be gained in many ways; experiments in the laboratory can allow us to understand nature better and nature can give us clues about where to look in those experiments. We can learn about nature by observing it directly, or by extrapolating from the known to the unknown. Eric Lerner says “The relationship between science in the laboratory and science in the cosmos runs in both directions. Many times important things about nature have been discovered by observing things in space.” This is the experience of his own work in plasma physics, where the plasma processes he studies in his laboratory are the counterparts of the processes seen in the galaxies.
A central problem with the theory of the Big Bang, he believes, is the assumption of an effect – the explosion of matter and energy into the universe – without a cause. For him this is the opposite of a scientific approach, which looks for the cause behind the effect. The power of science lies in its ability to generalise from observations and to make predictions – its ability to develop theory by studying the processes at work and then use that theory as a guide to action.
A creation myth
A further picture of the profound crisis that now exists for the Big Bang was given at the Portugal conference by Mike Disney in a paper titled “The insignificance of current cosmology”. He showed that current theories are based on an astonishingly small number of genuinely independent observations – he believes that at the most there are only five more independent observations than there are parameters in the theories. In his opinion:
“It can be argued there is little statistical significance to the good fits that impress conventional cosmologists… This same worrying situation has existed throughout the modern era of cosmology as the number of new parameters has expanded to accommodate the data.”
He has warned in the past about the dangers that exist in this situation:
“The most unhealthy aspect of cosmology is its unspoken parallel with religion. Both deal with big but probably unanswerable questions. The rapt audience, the media exposure, the big book-sale, tempt priests and rogues, as well as the gullible, like no other subject in science.”[7]
An uncomfortable parallel can be drawn between the Big Bang story and the Christian myth of creation. It is not sufficient to state, as do supporters of the Big Bang, that it is impossible to enquire what happened before the Big Bang – that there is no time before that time, and scientific enquiry, like everything else, must stop at that point. Mere mortals, sadly, cannot help but wonder. We only have to ask what initiated the explosion at the beginning of time to find that we are dragged back to the need for an initial impulse – the hand of God. In astrophysics this old idea comes dressed in modern clothes, but beneath them it remains medieaval in content. We are told that “quantum fluctuations”, supposedly a consequence of Heisenberg’s uncertainty principle, caused energy to appear for short periods, and triggered the birth of the universe.
Heisenberg’s uncertainty principle is a statement of how accurately we can simultaneously measure certain pairs of quantities such as momentum and position or time and energy. Yet uncertainty of knowledge, difficulties of observation, and our current limited understanding of wave-particle duality, do not imply ambiguities in physical reality. Quantum fluctuations are a mystical and idealistic interpretation of Heisenberg’s uncertainty principle taken out of context and devoid of physical content, in the tradition of the Copenhagen interpretation of quantum mechanics.[8]
It is a weak defence against the idealism and mysticism of religion to invoke an idealistic and mystical interpretation of quantum mechanics. Science increasingly has allowed us to find an explanation for natural phenomena, including the history and future of the universe, in material processes. God does not exist, there is no ghost in the machine, and we must look for God not in heaven but on Earth, in the reality of human existence. Human birth is a painful and traumatic experience. The scars show in the longing for that lost paradise, where literally “all is one”. In class society this basic fact of the human condition has its use as support for the rulers, the feudal landlord who appears for his rent with the priest in tow, the President and Prime Minister who excuse their terrorism by appealing to a higher authority, and then express God’s will in ton after ton of high explosive.
For the scientists of the alternative cosmology group the explanation for things that have occurred in the past lies in the processes that we see now, which in many cases we can explore in laboratory experiments. There is no effect without cause ‑ an infinite chain of cause and effect leads from now to the past. And for the plasma cosmologists the source of motion is matter itself, as described by the laws of electromagnetism.
This group of scientists are fighting to establish what is essentially a materialist and dialectical approach to the ideas of time and space and the origin of the universe. And they have done this because this is the only approach that conforms to the evidence. Eric Lerner says, for example:
“The universe never had an origin in time but it evolves… There doesn’t seem to be any evidence that the universe is finite in either space or time, which goes right back to what Giordano Bruno was burned at the stake for saying 400 years ago.”[9]
That the quantity of matter and motion is conserved in any process is a central and fundamental part of our knowledge of the physical world. And if matter and motion exist now then they always have and always will exist – not simply to the last syllable of recorded time but both before and beyond that time, whether recorded or not. For human beings to understand the abstraction infinity is difficult when it is so far outside of our experience and seems to have little practical meaning. Yet the existence now of matter and energy is the clearest evidence we have that they have always existed and always will. If we start with the physics that we know, then we have to conclude that the universe has no beginning, has no end, and that time is infinite.
But the universe is not static. Everywhere, at all scales, from the very small to the very large, there is change, motion and development. Galaxies, clusters of galaxies, evolve and change. Stars and planets are born, grow and die. Empires rise and fall against this backdrop. Individuals grow, learn, act and pass away. Within each individual billions of cells interact, grow, die and are renewed. And so on to the smallest scale and beyond. The human mind is the highest product of this process – as far as we know, as far as we can tell, in this small corner of the universe.
Appendix one: Critical Comment on Crisis in Cosmology
Nowhere in Harry Nielsen’s article, in “The Crisis in Cosmology”, Nov 24th 2005, does he seriously consider modern theories of inflationary cosmology with anything more than superficial misrepresentations.
In one passage Nielsen observes “Big Bang theorists have at several times in the history of the theory been forced to adjust their ideas when they have conflicted with new evidence”; isn’t this precisely what anyone using scientific methodology would be forced to do?
By comparison, Lerner and Co. have no coherent theory for the experimental observations. Whereas Gamow and others predicted the CMB 20 years before it was discovered by Penzias and Wilson, Lerner’s theories have not led to any serious predictions that have been experimentally verified.
Since Lerner assumes that the universe is infinitely old, but still evolving, he seems to be saying that the CMB radiation is a product of the endless scattering of electromagnetic radiation over infinite timescales. A simple question would be the one asked by Heinrich Olbers nearly two centuries ago: If this is so, why is the sky dark at night? Wouldn’t the effect of this endless scattering of light, x-rays and infra-red radiation be a much higher background temperature than is evident in the CMB today?
One very satisfying answer to Olbers’ paradox is of course, that we live in an expanding universe. The other is that distant light sources are too far away for their light to have reached us. Neither of these explanations is met if one assumes that stars and galaxies have existed for an infinite period of time. (Simply stretching the timescales is an evasion of the issue).
Similarly, the proportion of helium4 and deuterium observed in the universe agree very strongly with the model of a rapidly expanding and cooling cosmos. The figure of 25% for helium4 is closely in agreement with the predictions of Big Bang nucleosynthesis. The observed proportion of deuterium also strongly suggests that the universe is not infinitely old.
It’s certainly true that there are numerous things to be explained in the current inflationary model, such as dark matter and energy. You use the fact that they remained unexplained as evidence of “mysticism” and a stick to beat the theory with. A similar argument could be deployed against Einstein on the question of the cosmological constant! Does this invalidate Relativity?
The broad model of an inflationary universe agrees much more strongly with the evidence of observations than anything Lerner or his supporters have come up with. In fact, it is Lerner and Co. who are forced to take up arms against the laws of physics, by resorting vague and confusing statements like the following: -
“The data clearly show that the universe is not expanding, and that the redshift of light must be due to some other cause, perhaps in the properties of light itself.”
Think about this carefully. The proponents of the “standard model” of cosmology are attacked for introducing concepts which have yet to be fully explained, but agree with the experimental evidence. Lerner’s “explanation” would require a total re-write of the accepted laws of electromagnetism!
Mystifying matters even further, your article argues that: “One of the predictions from the inflationary theory is that the background radiation should be smooth apart from small random fluctuations. This prediction has been written into the textbooks, and has support from all the major proponents of the theory. Careful analysis of the WMAP results shows, however, that the radiation is not smooth.”
In fact, the theory predicts that the CMB is homogenous in all directions in space and behaves like a black body, which is borne out by the WMAP results. However, it also states that the fluctuations evident today reflect the effects of inflation on the tiny irregularities which existed in the earliest phase of the universe. These are generally explained by quantum effects occurring during the initial stages of inflation. Contrary to your claims, the WMAP observations don’t show anything which significantly conflicts with this model.
While it may be true that Big Bang theory has been used by some theorists to propose a metaphysical Creation “ex-nihilo” this is not a necessary feature of inflationary models since, as you must be well aware, but choose to ignore, many physicists working in the field of String Theory have developed models which do not require such a one-off event. In fact, String Theory could be described as a form of radical atomism, which defines matter and energy in a much more precise way than Quantum theory or General Relativity.
In some of the models developed by String theorists, a Big-Bang event can be the result of a sudden topological transition from an existing state of matter. This doesn’t necessarily require a singularity to be formed and thus avoids the infinities produced when trying to reconcile the Quantum theory and General Relativity. It implies that the “Constants of Nature” and the observable behaviour of the universe are determined for the current state of the universe by this event, but not necessarily that there was no preceding state.
You suggest that the lack of alternative theories to inflation is due to some academic conspiracy rather than the inherent weakness of alternatives, such as “Steady state” and Lerner & Alphen’s Plasma Astrophysics. It may be that electromagnetic plasmas play a role in the evolution of stars and galaxies which has been ignored in “conventional” cosmology, but nothing I have seen in all of their writings offers the explanatory power of inflationary theories synthesised with string theory, nor the possibility it offers of unifying sub-atomic physics with cosmology.
You choose to ride alongside them if you like, but I’m afraid this hobby horse is going up a dead-end on one wheel. I’m afraid it will all end in tears in the fabric of space-time!
November 27, 2005
Appendix two: Reply to comments on the article Crisis in Cosmology
It has been said many times that the method of Marxism is to first study the facts of a subject, and then to draw out its processes and its connections. This describes not only the method of Marxism but also the method of science (and Marxism is a science) - not to impose an arbitrary idea, but to study a subject from all angles and to find and generalise the underlying processes that are taking place. Then to use that theoretical insight as a guide to action, to learn from further experience, and to refine and develop the theory as a guide to further action.
This underlying reality of how human knowledge develops is today almost completely ignored in the theoretical physics and applied mathematics departments of the universities. The emphasis in modern physics is on deduction from axioms and on the development of ideas through mathematical logic. Ideas are placed ahead of observations and elegance in mathematical arguments is considered more important than evidence. Scientists pay lip-service to the idea that scientific “paradigms” – axioms and their associated concepts - are changed when contradicted by evidence. Yet the scientific hierarchy in the universities and the research funding bodies cling to the ideas that they have built their careers on long after those ideas have in reality been falsified.
The reply that we received to the recent article “Crisis in Cosmology” is a perfect example of the approach and attitudes that are prevalent amongst mainstream cosmologists and theoretical physicists. The most noticeable thing about the reply in fact is not what it says but what it doesn’t say. The writer simply ignores the evidence presented in the article – the recent observations which contradict the Big Bang:
The observed surface brightnesses of distant galaxies are several hundred times greater than predicted by the Big Bang expanding universe model.
The relative brightnesses of supernovae and the brightest galaxies in clusters of galaxies also contradict the expanding universe model.
The high-resolution map of the microwave background from the orbiting Wilkinson Microwave Anisotropy Probe (WMAP) shows a local component to the cosmic microwave background radiation, again in contradiction to the predictions of Big Bang theory.
Large-scale structures seen in clusters of distant galaxies would require three to six times longer to form than the time since the Big Bang.
Distant galaxies have been seen that predate the Big Bang by as much as one billion years.
Recent infra-red studies of the mass of the stars in galaxies and in clusters of galaxies show that visible matter can account for most of the observed gravitational effects, without the need for “dark matter”. (Dark matter, together with its counterpart “dark energy”, still remains undetected in any laboratory experiments).
The one topic in this list that he chooses to mention – the cosmic microwave background – he misrepresents by quoting only one paragraph of what was said in the article. Yes, the current Big Bang theory predicts random fluctuations in the microwave background. But the recent observations show variations that are far from random; there is a component of the radiation that is aligned with structures in the nearby universe such as the local supercluster of galaxies and perhaps even with the plane of the solar system, in clear contradiction to the predictions of the Big Bang.
A topic that was mentioned in passing in the article, and which the writer refers to in his reply, is the question of whether the Big Bang correctly predicts the proportions of various forms of helium and hydrogen and other light elements that are believed to exist in the universe. The writer repeats the usual assertion of Big Bang supporters that the observed ratios of these elements fit the Big Bang model. Again, the writer unfortunately didn’t pause to check the evidence before writing. If he had followed the reference given in the article to the proceedings of the Crisis in Cosmology conference he would have found that one of the presentations at the conference, from Tom van Flandern, was titled “The top problems with the Big Bang: the case of light elements”.[10] That paper raises again the serious discrepancies that exist between the predictions of the Big Bang and the actual observed ratios. Eric Lerner has also written on this topic and come to a similar conclusion – see the material on his website “The Big Bang Never Happened”.[11]
The writer adds one piece of evidence supposedly in support of the Big Bang: if the cosmic background radiation was caused by scattering, as the plasma physicists suggest, the sky would not be dark at night. This is an old conundrum, known as Olbers’ paradox, and which Big Bang supporters say shows the universe must be finite in time: the sky is dark because in some directions light from distant stars has not yet had the time to reach us since the beginning of the universe. Yet this is not the only possibility; a fractal distribution of material in the universe would also resolve the paradox. Complex scattering problems of this sort are just beginning to be looked at by physicists, in fields such as solid-state physics or geophysics, where wave energy is similarly scattered by random or fractal irregularities. They are an example of the non-linear type of processes that physics is only just beginning to understand and explore. This is an area which clearly needs more scientific work, as the writer almost certainly knows.
Much of the rest of the writer’s reply to the article consists of a plea for consideration of the “inflationary model” of the universe, which, with some variations, is the current version of the Big Bang theory. The writer believes that this theory has great predictive power, but the main point of the original article was to show that the predictions of the theory are increasingly being shown to be false. The theory has only survived either by ignoring the evidence (as the writer does) or by making arbitrary adjustments to its predictions as it has encountered new contradictions.
That ideas should change on the basis of new evidence, as the writer points out, is perfectly normal. But the process of arbitrary fix-ups, the addition of new variables, the invention of new physics (the inflaton, dark matter, dark energy, etc, etc) which has been used to allow the Big Bang theory to survive is something quite different. As Eric Lerner said last year in his letter to the New Scientist:
“In no other field of physics would this continual recourse to new hypothetical objects be accepted as a way of bridging the gap between theory and observation. It would, at the least, raise serious questions about the validity of the underlying theory.”[12]
It’s become acceptable in cosmology and in theoretical physics to make the most outlandish assertions (“many-sheeted space-time”; “the inflation-mediating inflaton”, “the many-world interpretation of wave-particle duality”, to mention a few) without the slightest piece of evidence. (They are axioms!) Often these ideas and their related mathematics contain so many arbitrarily adjustable variables that it is difficult to avoid the conclusion that for these researchers the evidence is merely an unavoidable nuisance, simply something to fit the theory to as an afterthought. This is not an exaggeration – Mike Disney’s presentation at the “Crisis in Cosmology” conference pointed out the worryingly small number of independent observations that are used to support current cosmological theory compared to the number of free variables. (“Fudge-factors” is the usual term used by researchers in those fields to describe the situation; anyone working in those areas who is honest with themselves will know that this is a perfectly accurate description of the prevailing method.) This may help to fill some chapters in a student’s PhD thesis, or perhaps provide the student’s supervisor with an idea for a popular science title, but it is not the method by which genuine scientific ideas are developed.
The writer feigns horror at Lerner’s suggestion that we may need to look for another explanation for the red-shift than the Doppler effect – saying that this would need “a total re-write of the accepted laws of electromagnetism”. (Maybe not a complete re-write – a couple of adjustable variables would do it.) But he should look at Lerner’s paper, which is available on his web-site, and see the way in which this experienced scientist reaches this conclusion after a thorough and careful examination of the data and the exclusion of other possibilities. There is a world of difference between this approach, with its respect for the data and its care at every step of the analysis, and the arbitrary mathematical constructions of the Big Bangers.
It is typical of the outlook of mainstream cosmologists that the plasma physicists and others from the alternative cosmology group are accused of having “no coherent theory for the experimental observations”. It’s to their credit in fact that some cosmologists at least have resisted the urge to make the type of sweeping statements that are so common in mainstream cosmology and instead have concentrated on a careful appraisal of the evidence and a cautious approach to theorising. When attempting to understand objects at such great distances for which there is in reality such a limited amount of information (primarily observations from different parts of the electromagnetic spectrum and little else), an attention to observational detail is the first requirement for genuine scientific work. Yet in Hannes Alfven’s work there are also many examples of explanation and insight into observed phenomena. These are based on physics that is known rather than physics that has been invented, and physics which it has been possible to investigate in the computer, as in the figure here, or in the laboratory.


Modern theoretical physics overwhelmingly emphasises deduction as the way to develop ideas about the universe, deriving predictions from more general ideas. But there is also another approach, philosophical induction, in which ideas and generalisations are derived from observations. Scientists, and Marxists, in reality use both approaches to learn about the world, from data to ideas and from ideas to data, working in both directions, simultaneously. First data (but according to an idea, a hypothesis to test, a direction to look), from which more ideas, then more tests, more ideas, and so on. This is induction and deduction, simultaneously, in parallel and in sequence – a union and interpenetration of opposites, out of which comes the growth and development of scientific ideas.
The fundamental problem with the Big Bang theory is its assumption of a beginning of time and an initial impulse. No amount of wriggling around – string theory, quantum fluctuations – can avoid this fundamental contradiction at the base of the theory. It’s inevitable that a theory based on false premises – that time has a beginning, that energy and matter can emerge from nothing – will fail experimental test. It is to Ted Grant and Alan Wood’s great credit that, more than 10 years ago now, they were able to identify and point to the errors and inconsistencies in the idea of the Big Bang. As time has gone by and more and more evidence has accumulated they have been shown to be absolutely correct in their analysis. This is a brilliant example of the power of dialectical materialism, which is not only a guide to political action but a general method of understanding nature and science. That the physicists in their ivory towers have on the other hand retreated into the clouds of mysticism and idealism is just a small example of the ideological decay of capitalist society, a symptom of impending revolution, not only in this part of science but in society as a whole.
December 4, 2005
Appendix three: Why is the sky not bright?
Dear comrades,
I agree with Harry Nielsen's reply to some criticisms of Alex Nichols on the article “Crisis in Cosmology”. But I feel there is one point that does deserve a more decisive counter-argument: the Olbers' paradox.
Heinrich Olbers stated that if galaxies and stars had existed for an infinite amount of time then the whole sky would look bright, not dark [at night]. Heinrich Olbers was right (at least if the Universe is not expanding fast enough and if it does not have a fractal shape).
Indeed, the Universe looks bright just not as bright as the Sun, because the Sun and the other stars are much warmer than the average temperature of the Universe. Every point of the sky is bright, at the typical wavelength of the Cosmic Background Radiation. It's just a wavelength our eyes cannot see: "an observer having his eyes sensitive to the Planck radiation at 3 K would see that the night sky is bright, as expected by Heinrich Olbers." (Paul Marmet, The 3K Microwave Background and the Olbers Paradox).
Nevertheless, plasma cosmology does not state that galaxies and stars have existed for an infinite amount of time. Eric J Lerner explained in his famous book “The Big Bang Never Happened” that stars came into existence at a certain stage of the development of the (infinitely old) Universe, something like 20 billion years ago. The Universe has always existed; galaxies and stars have not.
"The light has been turned on" in the Universe with the start of the nuclear age (fusion inside the stars), but we can't see the light of stars more than 20 billion light-years away. When we look so far we just see what was happening “before” the nuclear age, and those were much darker ages dominated by gravitation and electromagnetism.
If the pace of physical reactions transforming energy is getting faster and faster (and not slower and slower as the Big Bangers postulate), looking around us we would not see an infinitely intense light coming from every point: we would see a lot of light coming from nearer light-emitting spots and darkness when we look at places farther away everything covered by a halo of light resembling a 3K blackbody radiation, coming from the interstellar medium (mainly, plasma). Well, in fact that is what we actually see!
The infiniteness of the Universe in space and time is not paradoxical, particularly if we imagine it as an evolving universe, not a stationary one.
Mauro Vanetti, December 8, 2005
Pavia (Italy)
Appendix four: Could the universality of fractals in nature be a consequence of the dialectics of nature?
It's a very interesting comment from the comrade, and it's true that it could resolve Olbers' paradox - the question of why the night sky is not bright. Perhaps also what he suggests could have happened more than once, and in more than one place? If matter and hence time and space are infinite then the universe has already passed though an infinite number of states. Several of those states, an infinite number in fact, must also have had stars and galaxies that produced light. Following this line of thought, any event that has happened must in fact already have happened before, an infinite number of times, in an infinite number of places, and will happen again. The whole of history is pre-determined and we have no free will......
Here we've stumbled into a trap - the contradiction of infinity that philosophers and mathematicians have grappled with for thousands of years, from Zeno the Greek to the present day. A simple solution is to deny that the universe has existed for an infinite amount of time, as mainstream cosmologists have done. Ironically they draw this conclusion from the singularity in Einstein's equations - an infinity occupying zero time and space that supposedly exists at the origin of the universe. Then with suitable embellishments that adjust the theory to fit a few of the facts they claim to predict the development of the universe.
In another part of the physics department, perhaps across the university quadrangle, they would find physicists who have also faced the contradiction of infinity but with more success than the cosmologists. Through computer simulations these physicists have been able to show that complex non-linear systems - and a universe of infinite extent is a good candidate for this - can evolve and change for an infinite period of time without ever repeating. The earth's weather, for example, never repeats exactly. It is impossible to predict but it is not random; effect follows cause in every part of the system and in theory for infinite time. As it changes it can come close to states it has been in before; over an infinite period of time it may come infinitesimally close, but it will never repeat.
Physicists draw diagrams of “phase space” to analyse this behaviour. These are graphs that show the different states the system goes through; the path that the system goes along in phase space describes how the system is changing over time. In complex systems the patterns made by these paths are fractals - there is more and more detail at finer and finer scales. The system may come infinitesimally close to a position in phase space that it has been at previously but it will never come to exactly the same position. The universe can evolve for an infinite period of time but it will never repeat. History is not pre-determined, and is not determined mechanically at all, but is determined dialectically as a result of the many interactions between earth's billions of inhabitants. But it is not random; the underlying physical process is the development of production, now constrained and held back by the capitalist form of production, but it is this which pushes society forward in the same way that the sun's energy drives the weather.
It's possible, therefore, that the lights could have come on in the universe 20 billion or so years ago, as the comrade suggests, and prior to that time there was no light. As he says, this is consistent with a view of the universe that is infinite in time but which is evolving and not static. When we look far away we see what was happening earlier, and, as he says, it's possible “those were much darker ages dominated by gravitation and electromagnetism”. Perhaps there was a “change of state” on a cosmic scale, analogous to the change that occurs when ice forms from water, and the stars and galaxies then appeared.
But when we are trying to understand what has happened in the universe, we need to stay close to the evidence, and to what we know, if we are to avoid writing science fiction. Other than Olbers' paradox perhaps, is there any evidence that this is what has happened? Other than the idea of an infinite but continually evolving universe is there any known physics (meaning physics that has been established and tested) that could explain how or why this might happen? The idea does not seem to sit too well with Hannes Alfven's view that we should first try to use the physics that we know in order to explain the universe before inventing new physics. And is it a co-incidence that we are almost exactly repeating the words of the Christian myth of creation - “let there be light”?
The idea that the paradox can be resolved by a fractal distribution of the stars is discussed by the mathematician Benoit Mandelbrot in his book “The Fractal Geometry of Nature”. Since Mandelbrot's work in the 1960's there has been an increasing awareness of how prevalent fractals are in nature, and in society. They can describe rock layers in the earth, leaves on trees, river beds, income distributions, even the coast of Britain. (A famous paper from Mandelbrot is titled “How long is the coast of Britain?”, and he concludes that because coastlines are fractal the coast of Britain is infinitely long. Having walked part of the coastal path I can believe it.)
If the stars and galaxies have fractal geometry then we could expect clusters of galaxies, then clusters of clusters and so on. Similarly there would be voids in which there would be almost no stars or galaxies, some of which could come together to make bigger voids and then still bigger voids and so on. Mandelbrot points out that in that situation it is possible to find “a large proportion of directions that go to infinity without encountering any star”. So the sky will be dark at night.
The plasma physicists say that scattering of light by plasma clouds causes the background radiation. Strictly speaking this is different from the subject of Olbers' paradox, which talks about light from stars and not light from scattering. Supporters of the Big Bang would still argue though that the observed level of the radiation implies that the universe cannot be infinite in time because (quoting from Alex Nichol's letter) “the effect of this endless scattering of light, x-rays and infra-red radiation would be a much higher background temperature than is evident in the CMB today.”
Scattering by fractals (infinite scattering by infinite numbers of discontinuities at all scales) is a difficult topic and, as was mentioned in the reply to Alex Nichols, it has only recently been looked at in fields such as solid-state physics or geophysics where there are similar scattering problems. There does not seem to be anything in the scientific literature about Olbers' paradox and scattering by fractal clouds of plasma. Given the nature of fractals, it seems possible that a similar statement might apply in that case for the scattered light as for the direct light, but this is only a guess.
Possible support for the fractal idea as a way of resolving the paradox is that the universality of fractals in nature could be a consequence of the dialectics of nature. The scaling behaviour of fractals in nature, which links processes at many different scales, must be a symptom of the underlying general laws of change and motion - a symptom of the universality of the dialectical laws of change and development. Widely different processes can occur at different scales (the erosion of a small pebble from the sea-shore compared to the formation of bays and deltas), but a common geometry emerges because of the common dialectical behaviour.
Take the rocks in a cliff face for example. From a kilometre away it is possible to see a number of rock layers, and walking towards the cliff more layers will become visible. But the pattern of the layering (which could be quantified using suitable measurements) is the same at all scales, from the very large scale when viewing the layering at a large distance down to the scale of a few millimetres when close-up. (This is a controversial subject amongst geologists but does appear to be supported by the evidence.) How can this happen, when the small scale layering in the rocks was produced by completely different physical processes compared to the large layers?
This is another example of the complex dynamical problems that physicists have begun to study in the last 20 years or so. What the physicists are finding is what Hegel discovered several centuries ago - that changes in nature occur according to the general dialectical laws of motion. The small layers in the cliff face might be caused by changes in sedimentation rates; tectonic processes might cause the larger layers. But these different processes all produce layering with similar patterns because all these processes obey common dialectical laws of motion. Punctuated equilibria occur - at all scales. There is an accumulation of quantitative changes that produces sudden qualitative changes - at all scales. Necessity is expressed by chance - at all scales.
This is a paragraph from the article “Crisis in Cosmology” that mentions this:
“The reality of most physical phenomena is that there are many interlinked features, all of which interact. And increasingly physicists are beginning to find that it is the interaction that is more important than the details of the physical laws. Transitions occur that are determined by the complexity itself regardless of the details of the physics; this is why a fractal model can work over many scales and different physical mechanisms. The physical axioms and their deductions not only become inadequate, they become irrelevant. More general laws emerge - the dialectical laws of quantity and quality, of the union of opposites and the negation of the negation.”
Having said all this, there is only a limited amount of evidence that the universe might in fact have a fractal structure. There were some presentations at the “Crisis in Cosmology” conference on this topic, but the results were not convincing. Time will tell.
Comradely,
Harry Nielsen
Appendix five: Olbers' paradox
Olbers' paradox says that if the stars are uniformly distributed the sky will be lit nearly uniformly, day and the night, to a brightness similar to that of the Sun:
“When the light emitted by a star is proportional to its surface area, the amount of light reaching an observer at a distance R is proportional to 1/R2, but the star's apparent surface is itself proportional to 1/R2. Thus, the apparent ratio of light to spherical angle is independent of R. Also when the distribution of stars in the universe is uniform, almost any direction intersects some star. Therefore, the sky is uniformly bright, and seems ablaze. (The moons disc would form an exceptional dark domain, at least in the absence of atmospheric diffusion.)” From Mandelbrot, “The Fractal Geometry of Nature”.
The quote the comrade gives from the article by Paul Marmet appears to be wrong in saying that because of the cosmic background radiation “the night sky is bright as expected by Heinrich Olbers”. The background radiation in fact is much weaker than predicted by the paradox.
[1] See www.cosmology.info for further information on the alternative cosmology group and the “Crisis in Cosmology” conference; comments from Eric Lerner on recent cosmological observations are available at www.bigbangneverhappened.org
[2] The statement is available at www.cosmologystatement.org
[3] “Reason in Revolt”, Alan Woods and Ted Grant, 1995
[4] Guth’s work on cosmic inflation is pre-dated by James Blish's discovery of the Dillon-Wagoner “spindizzy”. This device is based on the Blackett-Dirac Equation, G2 = 8 P c /U where P is the magnetic moment of the body, c is the speed of light, and U is the angular momentum. By increasing U for every particle in a body, the constant of gravity is reduced. The concept was first described in the author’s novel Earthman Come Home (1950).
[5] An introduction to plasma cosmology is available at the author’s website www.electric-cosmos.org
[6] To hear the interview go to www.marxist.com/eric-lerner-interview050805.htm
[7] “The Case against Cosmology” [General Relativity and Gravitation, 32, 1125, 2000. astro-ph 009020]
[8] For more on this topic: “Against the Copenhagen interpretation of quantum mechanics – in defence of Marxism”.
[9] Heretical cosmologists and astronomers are no longer burned at the stake but are instead threatened with death by starvation. Academic researchers work on short-term 2 or 3-year contracts, with no guarantee of renewal. Even to step slightly outside the mainstream – merely to suggest, for example that the Hubble constant is moderately different from the accepted value and therefore the universe may be older than assumed by everyone else - is enough to put a person’s job at risk. Only if researchers show they can bring money into the university by attracting funding will they eventually after 5 years or often longer obtain a permanent contract. Academic funding in cosmology is decided by committees of experts who built their careers on the Big Bang theory; they rarely support research into alternatives.
[10] Abstracts of all the papers presented at the conference are available at www.cosmology.info
[11] See www.bigbangneverhappened.org
[12] The full statement is at www.cosmologystatement.org
[13] Extensive information on plasma cosmology is available from Peratt’s website The Plasma Universe

