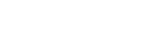Cuando tenemos una buena idea y la exageramos, en un momento dado, ésta se convierte en su contrario. Esto es lo que ha ocurrido con las conclusiones de los teóricos del Big Bang. Es muy común que cuando una idea da buenos resultados en el terreno de la ciencia, ésta se emplea en terrenos muy variados, pero ninguna idea es eterna en espacio-tiempo, de este modo llega un momento en que de tanto usarla, inevitablemente llega a un terreno donde no es válida, durante cierto tiempo los científicos no se percatan de ello, por lo tanto siguen empleando esta idea en ese terreno y en consecuencia obtienen resultados erróneos, que a pesar de ello los científicos consideran correctos, pero la realidad es concreta y por lo tanto revolucionaria. Los experimentos y resultados reales dan resultados muy distintos a los de estas teorías, esta contradicción hace revisar a los científicos sus teorías, de este modo se encuentran los defectos y forman una nueva teoría que vaya a la acorde de lo que ocurre en la realidad y al encontrarla generaliza a la anterior. Esto es lo que ha ocurrido con el Big Bang, esta teoría es una exageración de teorías correctas, tan exageradas que la teoría del Big Bang se convierte en su contrario, una teoría incorrecta.
Recta y curva aparecen equiparadas, en última instancia en el cálculo diferencial: en el triángulo diferencial, cuya hipotenusa forma la diferencial del cálculo (en el método tangencial), puede considerarse esta hipotenusa ``como una pequeña línea recta que es, al mismo tiempo, elemento del arco y elemento de la tangente'', ya se considere la curva como integrada por infinitas líneas rectas o se la considere ``como una curva fija; puesto que la curvatura es en cada punto
, infinitamente pequeña, no cabe duda de que la última relación existente entre el elemento de la curva y el de la tangente es una relación de igualdad''. Por tanto, también aquí, aunque la relación se acerca siempre a la igualdad, pero la naturaleza de la curva es siempre asintótica, puesto que el contacto se limita a un punto, carente de longitud, se acepta en última instancia que se ha llegado a la igualdad entre lo recto y lo curvo (Bossut, Calcul diff. et intégr., París, An VI, I, pág. 149). En las curvas polares, incluso se considera la abscisa imaginaria diferencial como paralela a la real, operándose en este sentido, aunque ambas se encuentran en el polo; más aún, se llega, partiendo de aquí, a la conclusión de que existe semejanza entre dos triángulos, uno de los cuales presenta un ángulo precisamente en el punto de intercesión de ambas líneas, sobre cuyo paralelismo se cifra toda la semejanza. Allí donde termina sobre poco más o menos la matemática de lo recto y lo curvo, se abre una nueva trayectoria, casi infinita con la matemática que concibe lo curvo como recto (triángulo diferencial) y lo recto como curvo (curva de primer grado, con una curvatura infinitamente pequeña). ¡Oh metafísica!
Dialéctica de la naturaleza
Federico Engels
Editorial Grijalbo
Pág. 226-227
Realmente la idea de Engels es mucho más profunda de lo que él mismo alcanzó a ver, ésta es la idea fundamental de la geometría diferencial local. Para la geometría diferencial local, un plano tangente en un punto P de una sábana es igual a la sábana muy cerca del punto ![]() . Nosotros entendemos por sábana cualquier conjunto que satisface lo siguiente: Para cualquier punto P de tal conjunto pasa un plano muy pequeño que es igual al conjunto muy cerca de éste, tal conjunto es una sábana. Ejemplo: La esfera, la silla de montar, el cilindro, la antena parabólica, el balón de fútbol americano, etc.
. Nosotros entendemos por sábana cualquier conjunto que satisface lo siguiente: Para cualquier punto P de tal conjunto pasa un plano muy pequeño que es igual al conjunto muy cerca de éste, tal conjunto es una sábana. Ejemplo: La esfera, la silla de montar, el cilindro, la antena parabólica, el balón de fútbol americano, etc.
 Figura 1: Esfera, silla de montar, cilindro, paraboloide, elipsoide
Figura 1: Esfera, silla de montar, cilindro, paraboloide, elipsoide
Noten lo siguiente: Todas las sábanas son iguales a un plano en cada uno de los puntos muy cerca de ellos mismos, pero ¡globalmente son muy diferentes! Es claro esto, ya que una silla de montar no es igual a un plano, tampoco lo es una esfera, sólo basta dimensionar el tamaño de nosotros, los seres humanos con respecto a este planeta, del que ocupamos una parte pequeñísima de su superficie y esa parte que ocupamos, es plana, es por ello que los antiguos pensaban que toda la tierra era plana.
Pero, ¿qué es lo que ocurre? ¿por qué no son iguales las sábanas a un plano globalmente? Esto se debe al carácter asintótico de la superficie con respecto al plano tangente. Como Engels explicó, podemos considerar a la sábana como la unión infinita de planos infinitamente pequeños, nótese que lo muy pequeño y lo muy grande se encuentran unidos. Un plano es un plano no una infinidad de planos como ocurre en una sábana es por ello que no son iguales el plano y la sábana. Más aún, entre las mismas sábanas no existe una relación de igualdad, un cilindro no es igual a una antena parabólica ¿por qué? Después de todo son la unión infinita de planos infinitamente pequeños. La respuesta es la siguiente. Aunque las superficies se encuentran formadas por una infinidad de planos, lo que las hace diferentes es el modo en como se encuentran unidos estos planos. Seguramente te debes estar haciendo la siguiente pregunta ¿podemos hacernos una idea de cómo se encuentran unidos los planos en un sábana? Reformulando esta pregunta, ¿podemos medir qué tanto se pandea una superficie?
 Figura 3: ``Cubrimiento'' con planos
Figura 3: ``Cubrimiento'' con planos
La respuesta a la anterior pregunta es afirmativa. Antes de empezar a responder esta pregunta debemos ponernos de acuerdo en cómo definiremos a un plano. En reconocer qué caracteriza a cada plano. Por un plano entenderemos al conjunto de todas las flechas que son perpendiculares a una flecha dada ![]() , a tal flecha la llamaremos flecha ortogonal y mide una unidad de longitud. Diremos que dos planos son paralelos si ambos planos tienen sus flechas ortogonales
, a tal flecha la llamaremos flecha ortogonal y mide una unidad de longitud. Diremos que dos planos son paralelos si ambos planos tienen sus flechas ortogonales ![]() y
y ![]() paralelas y diremos que se cortan con un ángulo
paralelas y diremos que se cortan con un ángulo ![]() si sus flechas ortogonales
si sus flechas ortogonales ![]() y
y ![]() forman un ángulo
forman un ángulo ![]() . Notemos que la flecha ortogonal
. Notemos que la flecha ortogonal ![]() caracteriza a cada plano que pasa por un punto
caracteriza a cada plano que pasa por un punto ![]() del espacio. Si dos planos pasan por un mismo punto y tienen sus flechas ortogonales paralelas, tales planos son iguales. De ahora en adelante a las flechas ortogonales
del espacio. Si dos planos pasan por un mismo punto y tienen sus flechas ortogonales paralelas, tales planos son iguales. De ahora en adelante a las flechas ortogonales ![]() las llamaremos flechas normales.
las llamaremos flechas normales.
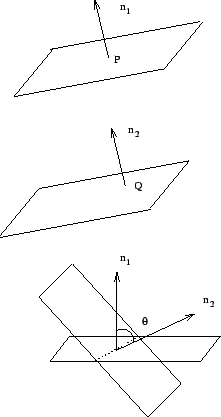 Figura 4: Ángulo entre dos planos
Figura 4: Ángulo entre dos planos Regresemos a las sábanas, escribimos arriba que éstas estaban formadas por una infinidad de planos y queríamos saber si es posible saber cómo podemos medir que tanto se pandea una sábana. Pues bien, fijémonos en una sábana y a tal sábana podemos fijarle las flechas normales a los planos que forman la superficie, de este modo estamos llenando de ``pelos'' a nuestra superficie. Nota que si tenemos una sábana lo que estamos haciendo es asociar a cada punto de esta sábana una flecha de tamaño de una unidad de longitud. Por otro lado, los puntos de la esfera de radio uno son flechas de una unidad de longitud. Por lo tanto, cuando le sacamos ``pelos''a nuestra sábana, lo que estamos haciendo es asociarle a cada punto de la sábana un punto de la esfera. A tal asociación le llamamos mapeo (aplicación) de Gauss en honor al matemático Karl F. Gauss. De este modo, cuando le sacamos ``pelos''a una región de la sábana, estamos pintando otra región de la esfera de radio uno. La región pintada es la región formada por las flechas normales a los planos de la sábana.
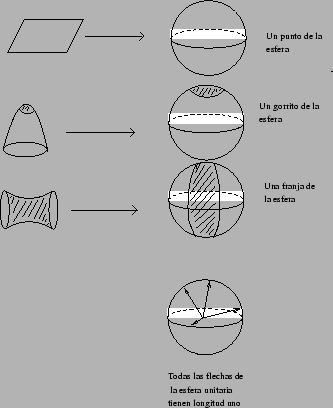 Figura 5: Aplicación de Gauss a distintas superficies
Figura 5: Aplicación de Gauss a distintas superficies De este modo cada sábana tiene su aplicación de Gauss o dicho de otro modo cada sábana tiene su propia forma de pintar la esfera. Este modo de pintar la esfera depende de cómo este curvada la sábana, pero el modo en cómo está pandeada la sábana depende de cómo están acomodados los planos que forman la sábana y esto es lo que hace el mapeo de Gauss, decirnos cómo están acomodados los planos. Ahora explicaremos cómo calcular cuantitativamente cómo se pandea una sábana en uno de sus puntos.
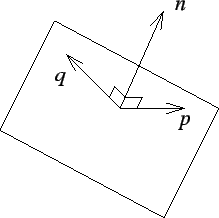 Figura 6: Vector normal a un plano
Figura 6: Vector normal a un plano Sea ![]() una sábana y sea
una sábana y sea ![]() un pedazo de
un pedazo de ![]() en el que se encuentra un punto
en el que se encuentra un punto ![]() de la sábana. Ahora calcularemos la aplicación de Gauss en el punto
de la sábana. Ahora calcularemos la aplicación de Gauss en el punto ![]() . Para ello calcularemos el mapeo de Gauss del pedazo
. Para ello calcularemos el mapeo de Gauss del pedazo ![]() , este será un casquete sobre la esfera, a tal casquete lo denotaremos como
, este será un casquete sobre la esfera, a tal casquete lo denotaremos como ![]() , después mediremos el área de este casquete, a tal número lo denotaremos como
, después mediremos el área de este casquete, a tal número lo denotaremos como ![]() . Después mediremos el área de
. Después mediremos el área de ![]() , este otro número lo denotaremos como
, este otro número lo denotaremos como ![]() . Definimos como curvatura
. Definimos como curvatura ![]() de la sábana en el punto
de la sábana en el punto ![]() a:
a:
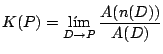
Esta formula significa que primero debemos calcular el área del casquete esférico ![]() y después el área de
y después el área de ![]() , después las dividimos y por último hacemos que el pedazo
, después las dividimos y por último hacemos que el pedazo ![]() se haga muy chico hasta que
se haga muy chico hasta que ![]() sea el punto
sea el punto ![]() . Cuando realizamos este proceso, el cociente de las áreas se va aproximando a un número, tal número es la curvatura. A esta altura de la monografía podemos empezar a sacar conclusiones con ayuda del materialismo dialéctico.
. Cuando realizamos este proceso, el cociente de las áreas se va aproximando a un número, tal número es la curvatura. A esta altura de la monografía podemos empezar a sacar conclusiones con ayuda del materialismo dialéctico.
- No está demás destacar la relación que hay entre lo curvo y lo plano. Una infinidad de planos infinitamente pequeños que forman una sábana curva ¡Mágico! ¡Contradictorio! ¡Dialéctico!
- Para aquellos que recuerden la definición de la derivada (si no, les recomendamos leer el artículo Cálculo y materialismo, Fundación Federico Engels), habrán observado, y de manera muy atinada, que la forma de la curvatura es muy similar a la de la derivada, en este último caso, la derivada mide la razón de cambio entre la imagen y el dominio de una función, con la curvatura sucede algo análogo, y es que en cierta forma lo que está midiendo la curvatura es la razón de cambio entre la imagen en la aplicación de Gauss en la esfera y el pedazo de sábana, que en este caso juega el papel del dominio.
- De lo anterior se desprende que el concepto de curvatura es una contradicción porque ésta nos mide qué tanto se pandean los planos de las sábanas, que en principio no se pandean (ver cita de Engels).
Geometría diferencial global de las sábanas. Teorema de Gauss-Bonnet
Todo lo tratado arriba es referente a la teoría local de las sábanas ya que en esta parte se ha usado fuertemente el hecho de que la curva y la recta son iguales muy cerca del punto, pero globalmente esto es falso. Una sábana no sigue estas mismas leyes, sigue otras leyes porque globalmente una sábana no necesariamente es un plano.
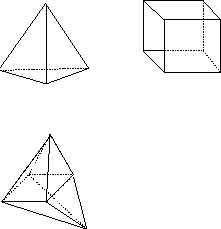 Figura 7: Poliedros
Figura 7: Poliedros Leonard Euler descubrió que todos los poliedros satisfacen lo siguiente: Si ![]() es el número de vértices,
es el número de vértices, ![]() el número de aristas y
el número de aristas y ![]() el número de caras de un poliedro, en tal caso se cumple la siguiente identidad:
el número de caras de un poliedro, en tal caso se cumple la siguiente identidad:
![]()
A tal fórmula la llamamos característica de Euler para los poliedros. (ver figura y tabla). En general denotaremos la fórmula de Euler para un poliedro ![]() de la siguiente manera:
de la siguiente manera:
![]()
A este número ![]() lo llamamos característica de Euler del poliedro
lo llamamos característica de Euler del poliedro ![]() . Más abajo generalizaremos este concepto para sábanas. Pero, ¿cuál es la característica de Euler para las donas cuadradas? (ver figura).
. Más abajo generalizaremos este concepto para sábanas. Pero, ¿cuál es la característica de Euler para las donas cuadradas? (ver figura).
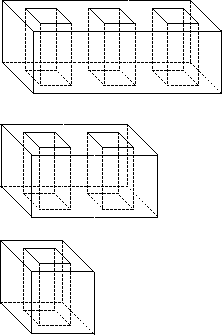 Figura 8: ``Toros'' cúbicos
Figura 8: ``Toros'' cúbicos Para tales poliedros ![]() la característica de Euler está dada por:
la característica de Euler está dada por:
![]()
Donde ![]() indica el número de hoyos que tiene el poliedro, lo que nos interesa de la característica de Euler es lo siguiente: ¡la característica de Euler es un invariante topológico! ¿qué significa esto? Para explicar esto, primero tenemos que explicar que significa que dos figuras sean ``topológicamente iguales''. Primero tomemos una figura hecha de plastilina, por ejemplo un cubo. Nosotros podemos tomar este cubo y empezar a moldear otra figura final deformando la inicial. Diremos que la figura inicial es topológicamente igual a la figura final siempre que al tomar cualesquiera dos puntos cercanos de la figura inicial sigan siendo cercanos en la figura final después de haber moldeado la otra figura.
indica el número de hoyos que tiene el poliedro, lo que nos interesa de la característica de Euler es lo siguiente: ¡la característica de Euler es un invariante topológico! ¿qué significa esto? Para explicar esto, primero tenemos que explicar que significa que dos figuras sean ``topológicamente iguales''. Primero tomemos una figura hecha de plastilina, por ejemplo un cubo. Nosotros podemos tomar este cubo y empezar a moldear otra figura final deformando la inicial. Diremos que la figura inicial es topológicamente igual a la figura final siempre que al tomar cualesquiera dos puntos cercanos de la figura inicial sigan siendo cercanos en la figura final después de haber moldeado la otra figura.
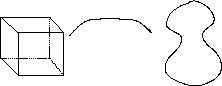 Figura 9: Transformación continua
Figura 9: Transformación continua Un ejemplo de dos figuras que no son iguales topológicamente son las que presentan ruptura. (ver figura 10)
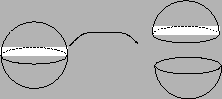 Figura 10: Transformación discontinua
Figura 10: Transformación discontinua Ya estamos en condiciones de explicar que significa que la característica de Euler es un invariante topológico. Sean ![]() y
y ![]() dos figuras iguales topológicamente en tal caso
dos figuras iguales topológicamente en tal caso ![]() . Es decir, la característica de Euler es la misma para figuras topológicamente iguales.
. Es decir, la característica de Euler es la misma para figuras topológicamente iguales.
Ejemplo 1:
El cubo y la esfera son topológicamente iguales, por lo tanto la característica de Euler de la esfera es igual a la del cubo, pero por lo escrito arriba, la característica de Euler del cubo es ![]() , por lo tanto la característica de Euler de la esfera también es
, por lo tanto la característica de Euler de la esfera también es ![]() , porque la esfera es un cubo inflado.
, porque la esfera es un cubo inflado.
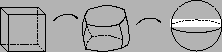 Figura 11: La esfera es un ``cubo inflado''
Figura 11: La esfera es un ``cubo inflado'' Ejemplo 2:
La característica de Euler de la dona es cero porque el cubo con un hoyo es topológicamente igual a la dona y por lo escrito arriba, la característica de Euler con un hoyo es cero. Vale la pena que definamos aquí un nuevo concepto de curvatura, lo llamaremos curvatura total de la sábana. La curvatura total de la sábana ![]() es el área del casquete formado en la esfera por la aplicación de Gauss. Denotaremos la curvatura total mediante la letra griega
es el área del casquete formado en la esfera por la aplicación de Gauss. Denotaremos la curvatura total mediante la letra griega ![]() .
.
Ejemplo 3:
Si ![]() es un plano, Su mapeo de Gauss es sólo un punto de la esfera. Como tal punto tiene un área cero en la esfera podemos decir que la curvatura total del plano
es un plano, Su mapeo de Gauss es sólo un punto de la esfera. Como tal punto tiene un área cero en la esfera podemos decir que la curvatura total del plano ![]() es cero.
es cero.
Ejemplo 4: La curvatura total de la esfera es ![]() . Porque el área barrida por las flechas ortogonales de la esfera (el mapeo de Gauss) es una esfera de radio
. Porque el área barrida por las flechas ortogonales de la esfera (el mapeo de Gauss) es una esfera de radio ![]() y el área de ésta es
y el área de ésta es ![]() .
.
A esta altura de la monografía vale la pena detenernos para sacar nuevas conclusiones. La igualdad topológica lo que realmente nos dice es que dos sábanas son cualitativamente iguales, por lo tanto la característica de Euler es una propiedad cualitativa de las sábanas. Mientras que la curvatura total es una propiedad cuantitativa de las sábanas. En este sentido la característica de Euler ![]() y la curvatura total
y la curvatura total ![]() de una sábana
de una sábana ![]() son contrarios ya que el primero representa una propiedad cualitativa y la segunda una propiedad cuantitativa. La dialéctica nos enseña que los contrarios luchan y se mantienen unidos, que la calidad se convierte en cantidad y viceversa. Esta es la enseñanza que nos deja el Teorema de Gauss-Bonnet, que según varios autores es el más bello de toda la geometría diferencial.
son contrarios ya que el primero representa una propiedad cualitativa y la segunda una propiedad cuantitativa. La dialéctica nos enseña que los contrarios luchan y se mantienen unidos, que la calidad se convierte en cantidad y viceversa. Esta es la enseñanza que nos deja el Teorema de Gauss-Bonnet, que según varios autores es el más bello de toda la geometría diferencial.
Teorema de Gauss-Bonnet
Sea ![]() una sábana formada por una pieza, cerrada y que no se extiende de manera infinita. En tal caso
una sábana formada por una pieza, cerrada y que no se extiende de manera infinita. En tal caso
![]()
Vale la pena notar que este teorema es un Teorema Global, es decir, esta identidad es válida en todas las sábanas y no sólo para pequeñas partes de la sábana como sucedía arriba.
Algunos aspectos históricos acerca del teorema de Gauss-Bonnet
Ya antes expliqué que no es lineal el modo en que llegamos a plantear los teoremas y ecuaciones en matemáticas, los planteamientos y lemas se hacen a través de aproximaciones sucesivas, además, estas aproximaciones no siguen un camino recto al teorema principal, el camino a estos resultados está lleno de caídas, retroceso y empujones; esto también ocurrió con el teorema de Gauss-Bonnet, ya que antes del teorema de Gauss-Bonnet, tenemos otros teoremas que nos sirven como puente para llegar a éste, estos teoremas ``puente'', son un fin, en el sentido de que el planteamiento de estos, son el planteamiento más acabado de otros lemas y teoremas, pero también son ``puentes'', o mejor dicho, un medio para abordar un nuevo teorema, de este modo, todos los teoremas son fin y medio a la vez. Es cierto que en los libros se presenta una formulación de los problemas, siguiendo una línea recta rumbo al teorema principal, pero esto se debe a que el autor de tal libro, lo plantea de este modo para que el lector entienda con mayor facilidad lo planteado y el camino hacia el ``teorema final'', pero incluso en casi todos los libros de texto, cuando intentamos llegar a un resultado, esto se suele hacer a partir de aproximaciones sucesivas, aunque en estos, se sigue un orden cognoscitivo.
Para concluir esta sección, señalaremos que de acuerdo con Gottlieb, existen algunos resultados de Descartes publicados en 1860 y Dyck en 1888, que extienden los teoremas de Gauss-Bonnet y observan por vez primera la relación entre la integral de la curva gaussiana y la característica de Euler-Poincaré. En este sentido, Gottlieb sugiere que el conocido teorema de Gauss-Bonnet debería ser llamado teorema de Descartes-Dyck. Este es un caso más en la historia donde se conjuga el esfuerzo de muchas personas, aunque sólo una o dos de ellas se conviertan en parte integral del nombre de un resultado.
Reyes, J.G. Palmas, O. Curso de geometría diferencial II. Geometría intrínseca de las superficies
Los errores de la teoría del Big Bang
Cuando tenemos una buena idea y la exageramos, en un momento dado, ésta se convierte en su contrario. Esto es lo que ha ocurrido con las conclusiones de los teóricos del Big Bang. Es muy común que cuando una idea da buenos resultados en el terreno de la ciencia, ésta se emplea en terrenos muy variados, pero ninguna idea es eterna en espacio-tiempo, de este modo llega un momento en que de tanto usarla, inevitablemente llega a un terreno donde no es válida, durante cierto tiempo los científicos no se percatan de ello, por lo tanto siguen empleando esta idea en ese terreno y en consecuencia obtienen resultados erróneos, que a pesar de ello los científicos consideran correctos, pero la realidad es concreta y por lo tanto revolucionaria. Los experimentos y resultados reales dan resultados muy distintos a los de estas teorías, esta contradicción hace revisar a los científicos sus teorías, de este modo se encuentran los defectos y forman una nueva teoría que vaya a la acorde de lo que ocurre en la realidad y al encontrarla generaliza a la anterior. Esto es lo que ha ocurrido con el Big Bang, esta teoría es una exageración de teorías correctas, tan exageradas que la teoría del Big Bang se convierte en su contrario, una teoría incorrecta. El problema que da origen a la relatividad original es el siguiente. Mercurio forma rosetas al girar alrededor del sol (ver figura 12). Pero la teoría newtoniana no brinda la trayectoria correcta, de esta forma, tal teoría queda rezagada.
Einstein en 1915 resuelve el problema, y esta solución da como origen a la Teoría General de la Relatividad. Para resolver este problema y en consecuencia para entender la Teoría General de la Relatividad es necesario emplear los métodos de la geometría diferencial. Con ayuda de este aparato, Einstein deduce una ecuación llamada ecuación de Einstein que permite encontrar la solución al problema de Mercurio.
 Figura 12: Trayectoria de la órbita del planeta Mercurio
Figura 12: Trayectoria de la órbita del planeta Mercurio Los científicos motivados por el poder de la nueva teoría la siguen empleando para seguir sus dudas, y en efecto, esta nueva perspectiva les abre camino no sólo para resolver sus viejas dudas, también para empezar una nueva teoría que explique los fenómenos gravitatorios, que la teoría newtoniana no explica. Pero al modelar la teoría gravitatoria ellos emplean la geometría diferencial local, misma de la que se basa Einstein para sacar sus conclusiones correctas, el problema de esto es que cuando ellos llegan a sacar un resultado lo generalizan como un resultado válido para todo el universo y no como un resultado de validez local, si Einstein pudo llegar a resultados correctos es porque él uso localmente sus resultados, la distancia entre mercurio y el sol es infinitamente pequeña comparado con todo el universo, por lo tanto es válido usar la geometría diferencial local, pero cuando nosotros queremos sacar conclusiones globales, es decir, válidas en todo el universo, nosotros debemos emplear la geometría diferencial global. Cosa que no emplean nuestros científicos y físicos teóricos. El cometer este error, es decir, usar la geometría diferencial local en lugar de la geometría diferencial global para sacar conclusiones válidas, es equivalente a decir que un plano y una esfera son iguales ¡como cuando los antiguos creían que la tierra era plana! Basados en este error, los cosmólogos llegan a conclusiones como la del Big Bang.